Answer: Our required 98% confidence interval would be (53.51,246.49).
Explanation:
Since we have given that
Sample of joints from species A = 120
Mean of shear stress = 1250 psi
Standard deviation = 350 psi
Sample of joints from species B = 90
Mean = 1400 psi
Standard deviation = 250 psi
98% confidence interval
α = 100 -98 = 2%
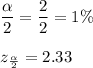
98% confidence interval would be

Hence, our required 98% confidence interval would be (53.51,246.49).