Question

If the resultant of two velocity vectors of equal magnitude is also of the same magnitude, then which statement must be correct?

A) The two velocity vectors are antiparallel.
Eliminate
B) The angle between the vectors is 60°.
C) The angle between the vectors is 120°.
D) The two velocity vectors are parallel to each other.

Answer 1

The correct option is C) The angle between the vectors is 120°.

Why?

We can solve the problem and find the correct option using the Law of Cosine.

Let A and B, the given two sides and R the resultant (sum),

Then,

`R=A=B`

So, using the law of cosines, we have:

`R^(2)=A^(2)+B^(2)+2ABCos(\alpha)\\ \\A^(2)=A^(2)+A^(2)+2*A*A*Cos(\alpha)\\\\0=A^(2)+2*A^(2)*Cos(\alpha)\\\\Cos(\alpha)=-(A^(2))/(2*A^(2))=-(1)/(2)\\\\\alpha =Cos(-(1)/(2))^(-1)=120\°`

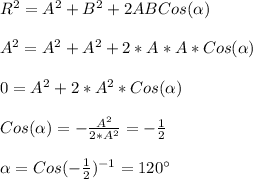
Hence, we have that the angle between the vectors is 120°. The correct option is C) The angle between the vectors is 120°

Have a nice day!