Question

Consider a game in which a fair die is rolled. If the die comes up 1, the player wins $2. If the die comes up 2, the player wins $1. For all other outcomes, the player loses $1. What is the expected amount that the player wins or loses? Round to the nearest cent.

Answer 1

The expected value for this game is approximately -$0.17, indicating an expected average loss of $0.17 per game.

Step-by-step explanation:

The expected amount that the player wins or loses in this game can be calculated using the formula for expected value, which involves multiplying each possible outcome by its probability and summing the results. In this case, the player wins $2 with a probability of 1/6, wins $1 with a probability of 1/6, and loses $1 with a probability of 4/6.

Therefore, the expected value can be calculated as:

(2 * 1/6) + (1 * 1/6) + (-1 * 4/6) = -0.1667.

So, the player is expected to lose approximately $0.17 per game.

Answer 2

Expected amount is loss of 0.167 $.

Step-by-step explanation:

Probability is the ratio of number of favorable outcome to total number of outcomes.

Total number of outcomes = 6, since the die has 6 faces.

`\texttt{Probability of getting 1 =}(1)/(6)\\\\\texttt{Probability of getting 2 =}(1)/(6)\\\\\texttt{Probability of getting numbers except 1 and 2 =}(6-2)/(6)=(4)/(6)=(2)/(3)`

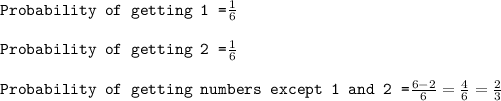
If the die comes up 1, the player wins $2. If the die comes up 2, the player wins $1. For all other outcomes, the player loses $1.

Now we need to find expected amount that the player wins or loses.

Expected amount = ∑Probability of event x Winning or losing on that event

`\texttt{Expected amount =}(1)/(6)* 2+(1)/(6)* 1-(2)/(3)* 1=(2+1-4)/(6)=(-1)/(6)=-0.167\$`

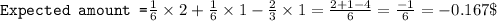
Expected amount is loss of 0.167 $.