Question

According to the Entertainment Software Association, the average age of "gamers" (those that routinely play video games) is 30 years old. A random sample of 33 gamers people had an average age of 32.7 years old. Assume that the population standard deviation for the age of gamers is 4.6 years. Use a 90% confidence interval to test the validity of this report and choose the one statement that is correct. A) Because this confidence interval does not include 30 years, the report by the Entertainment Software Association is not validated. B) Because this confidence interval does not include 30 years, the report by the Entertainment Software Association is validated. C) Because this confidence interval does include 30 years, the report by the Entertainment Software Association is validated. D) Because this confidence interval does include 30 years, the report by the Entertainment Software Association is not validated.

Answer 1

A) Because this confidence interval does not include 30 years, the report by the Entertainment Software Association is not validated.

Explanation:

We are given the following information in the question:

n = 33

Sample mean = 32.7 years

Population mean = 30 years

Population standard deviation = 4.6 years

Significance level = 90%

Formula:

`\bar{x} \pm z_(critical)(s)/(√(n))`

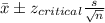
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.10) = 1.28`

`32.7 \pm 1.28((4.6)/(√(33)) ) = 32.7 \pm 1.024 = (31.676,33.724)`

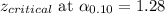
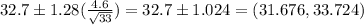
It is clear that the population mean that is 30 years does not belong to this confidence interval.

A) Because this confidence interval does not include 30 years, the report by the Entertainment Software Association is not validated.