Question

This is a reaction going on in your muscle cells right this very minute:The enzyme triose phosphate isomerase catalyzes this reaction in the forward direction as part of the glycolyticpathway. It follows simple Michaelis-Menten kinetics:Typical cellular concentrations: triose phosphate isomerase = 0.1 nMdihydroxyacetone phosphate = 5 μM glyceraldehyde-3-phosphate = 2 μM48. Refer to Exhibit A. What is the actual velocity of the forward reaction under physiologic conditions if KM = 10 μM?

Answer 1

Step-by-step explanation:

The given reaction is as follows.

`E + S \rightleftharpoons ES \xrightarrow[]{k_(2)} E + P`

Here, [E] = triose phosphate isomerase = 0.1
`nm = 0.1 * 10^(-9)m`

[S] = Dihydroxy acetone phosphate = 5
`\mu m = 5 * 10^(-6)m`

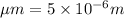
[P] = Glyceraldehyde-3-phosphate = 2
`\mu m = 2 * 10^(-6)m`

Therefore, velocity of the reaction will be as follows.

v =
`(d[P])/(dt)` =
`(K_(2)[E][S])/(K_(M) + [S])`

where,
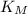`K_(M)` = Michaelic menten constant =
`(K_(1) + K_(2))/(K_(1))`

v =
`(900 * 0.1 * 10^(-9)m * 5 * 10^(-6)m)/(10^(-5) + 5 * 10^(-6))`

=
`30 * 10^(-9) m`

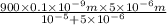
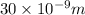
or, = 30 nm/s

Hence, we can conclude that the actual velocity of the forward reaction under physiologic conditions if KM = 10 μM is 30 nm/s.