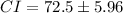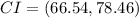Answer:
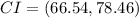
Explanation:
Given : A new catalyst is being investigated for use in the production of a plastic chemical. Ten batches of the chemical are produced. The mean yield of the 10 batches is 72.5% and the standard deviation is 5.8%. Assume the yields are independent and approximately normally distributed.
To find : A 99% confidence interval for the mean yield when the new catalyst is used ?
Solution :
Let X be the yield of the batches.
We have given, n=10 ,
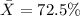 , s=5.8%
, s=5.8%
Since the size of the sample is small.
We will use the student's t statistic to construct a 995 confidence interval.
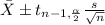
From the t-table with 9 degree of freedom for
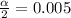
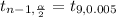

The 99% confidence interval is given by,