Question

A rare coin appreciates at a rate of 5.2% a year. If the initial value of the coin is $500, after how many years will its

value cross the $3,000 mark? Show the formula that models the value of the coin after t years.

Answer 1

Answer: 36 years

Explanation:

Exponential equation to represent growth:-

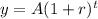`y=A(1+r)^t` , where A is the initial value , r is the rate of growth and t is the time period.

Given : A rare coin appreciates at a rate of 5.2% a year. If the initial value of the coin is $500.

i.e. Put A= 500 and r= 0.052 in the above formula.

The amount after t years:

`y=500(1.052)^t`

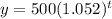
Inequality for value cross $3,000 mark:

`3000<500(1.052)^t`

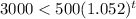
Divide both sides by 500

`6<(1.052)^t`

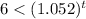
Taking log on both sides , we get

`\log6<t\ \log(1.052)\\\\=0.778151250384< t(0.0220157398177)\\\\ t>(0.778151250384)/(0.0220157398177)=35.345223773\\\\t\approx36`

Hence, it will take approx 36 years to cross the $3,000 mark.