Question

Find the common ratio and an explicit form in each of the following geometric sequences.

c.4 / 3,2 / 3,1 / 3,1 / 6 , ...

Answer 1

The common ratio is
`(1)/(2)` and the explicit form is
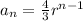`a_(n) =(4)/(3)r ^(n-1)` for all n≥1.

Explanation:

The general form of a geometric sequence is
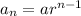`a_(n)=ar^(n-1)`, for all n≥1, where r≠0 is the common ratio and
`a` is the first term of the sequence.

From the problem we know the first term is a=
`(4)/(3)`, so we only need to calculate r. We know that
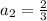`a_(2) =(2)/(3)` is the second term of the sequence, so we can replace
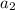`a_(2)` and a into our formula and find the value of r, so we have for n=2

`a_2=ar^(2-1)`

`(2)/(3) =(4)/(3) r`

`r=((2)/(3) )/((4)/(3) )=(2)/(4)=(1)/(2)`

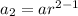
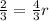
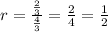
so the explicit form is
`a_(n)=a((1)/(2))^(n-1)` for all n≥1, where
`a=(4)/(3)`

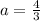
We can check the general formula by substituting the values into the equation.

`a_1=((4)/(3) )((1)/(2) ^(1-1))=((4)/(3))(1)=(4)/(3) =a`

`a_2=((4)/(3) )((1)/(2) )^(2-1)=((4)/(3))((1)/(2) )=(2)/(3)`

`a_3=((4)/(3) )((1)/(2) )^(3-1)=((4)/(3))((1)/(2)^(2) )=((4)/(3))((1)/(4))=(1)/(3)`

`a_4=((4)/(3) )((1)/(2) )^(4-1)=((4)/(3))((1)/(2)^(3) )=((4)/(3))((1)/(8))=(1)/(6)`

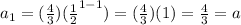
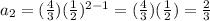
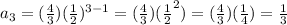
We can conclude that the explicit form of the geometric sequence is
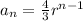`a_(n) =(4)/(3)r ^(n-1)` for all n≥1, and the common ratio is
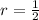`r=(1)/(2)`.