Question

Tarzan swings on a 26.2 m long vine initially inclined at an angle of 28° from the vertical. (a) What is his speed at the bottom of the swing if he starts from rest? m/s (b) What is his speed at the bottom of the swing if he starts with an initial speed of 3.00 m/s? m/s

Answer 1

given,

length of the swing = 26.2 m

inclined at an angle = 28°

let, the initial height of the Tarzan be h

h = L (1 - cos θ)

a) initial velocity v₁ = 0 m/s

final velocity of Tarzan = v_f

law of conservation of energy

PE_i + KE_i = PE_f + KE_f

`mgh_i + (1)/(2)mv_i^2= mgh_f + (1)/(2)mv_f^2`

`mgh_i + 0 = 0 + (1)/(2)mv_f^2`

`mgh_i = (1)/(2)mv_f^2`

`v_f = √(2gh_i)`

`= √(2gL(1- cos\theta))`

`= √(2* 9.8 * 26.2(1- cos 28^0))`

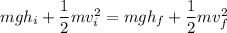
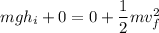
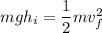
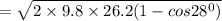
= 7.75 m/s

the speed tarzan at the bottom of the swing

v_f = 7.75 m/s

b)initial speed of the = 3 m/s

`mgh_i + (1)/(2)mv_i^2= mgh_f + (1)/(2)mv_f^2`

`mgh_i + 0 = 0 + (1)/(2)mv_f^2`

`mgh_i+ (1)/(2)mv_i^2 = (1)/(2)mv_f^2`

`gh_i+ (1)/(2)v_i^2 = (1)/(2)v_f^2`

`v_f = √(v_1^2+2gh_i)`

`v_f = √(3^2+2* 9.8 * (1- cos 28^0))`

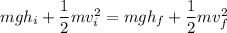
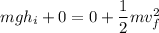
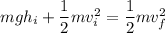
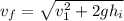
v_f= 11.29 m/s