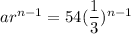Question

The first term in a geometric sequence is 54, and the 5th term is 2 / 3. Find an explicit form for the geometric sequence.

Answer 1

Answer:
`ar^(n-1)=54((1)/(3))^(n-1)`

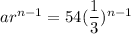
Explanation:

The nth term for a geometric sequence is given by :-

`a_n=ar^(n-1)` (1)

We are given that The first term in a geometric sequence is 54. i.e. a=54

5th term=
`(2)/(3)` (2)

Put n=5 and a= 54 in (1), we get

`a_5=(54)r^(4)=` (3)

From (2) and (3), we have

`\Rightarrow(54)r^(4)=(2)/(3)\\\\\Rightarrow r^4=(2)/(3)*(1)/(54)=(1)/(3*27)=(1)/(81)\\\\\Rightarrow\ r=((1)/(81))^{(1)/(4)}=(1)/(3)`

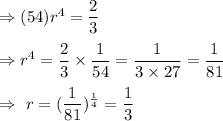
Explicit form for the geometric sequence:
`ar^(n-1)=54((1)/(3))^(n-1)`