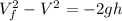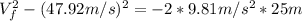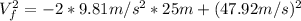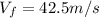Question

A pitcher throws a 0.140 kg baseball, and it approaches the bat at a speed of 35.0 m/s. The bat does Wnc = 75.0 J of work on the ball in hitting it. Ignoring air resistance, determine the speed of the ball after the ball leaves the bat and is 25.0 m above the point of impact.(Answer in m/s)

Answer 1

The speed of the ball is 42.5 m/s

Step-by-step explanation:

The initial kinetic energy of the ball is:

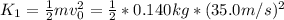`K_1=(1)/(2) m v_0^2=(1)/(2)*0.140 kg*(35.0 m/s)^2`= 85.75 J

The speed of the ball after leaving the bat is:

`K_2=K_1+W_(nc)\\ (1)/(2)mV^2= 85.75 J + 75 J\\ ((1)/(2)mV^2)2=( 160.75 J)2\\ mV^2= 321.5 J\\ V^2= (321.5 J)/(0.140kg) \\ V=\sqrt{(321.5 J)/(0.140kg)}`

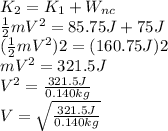
V=47.92 m/s

Using kinematic equation we can find the speed of the ball after being 25 m above the point of collision:

`V_f^2-V^2=-2gh`

`V_f^2-(47.92 m/s)^2=-2*9.81m/s^2*25m`

`V_f^2=-2*9.81m/s^2*25m+(47.92 m/s)^2`

`V_f=√(-2*9.81m/s^2*25m+(47.92 m/s)^2)`

`V_f=42.5m/s`