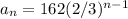Answer:
The explicit form is
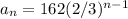
Explanation:
The explicit form of a geometric sequence is given by:
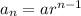
where an is the nth term, a is the first term of the sequence and r is the common ratio.
In this case:
a=162
The value of the common ratio is obtained by dividing one term by the previous term.
For the first and second terms:
108/162=2/3
For the second and third terms (In order to prove that 2/3 is the common ratio)
72/108=2/3
Therefore:
r=2/3
Replacing a and r in the formula: