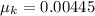Answer:
At low pressure-
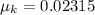
At high pressure-
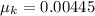
Step-by-step explanation:
Initial speed,
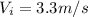
Final speed,
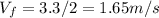
Net horizontal force due to rolling friction
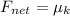 mg where m is mass, g is acceleration due to gravity,
mg where m is mass, g is acceleration due to gravity,
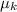 is coefficient of rolling friction
is coefficient of rolling friction
From kinematic relation,
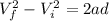
For each tire,
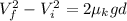
Making
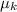 the subject
the subject
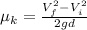
Under low pressure of 40 Psi, d=18 m
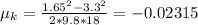
Therefore,
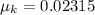
At a pressure of 105 Psi, d=93.7
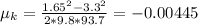
Therefore,