Answer:
The explicit form for this sequence is
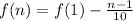 for all
for all
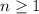 .
.
Explanation:
The explicit form of an arithmetic sequence of numbers is given by the formula
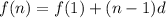 , where
, where
 is the first term of the sequence,
is the first term of the sequence,
 is the difference between two consecutive terms of the sequence, and
is the difference between two consecutive terms of the sequence, and
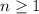 .
.
We know that the first four elements for the arithmetic sequence are
 .
.
To find the general formula for this problem we only need to calculate
 in the above formula.
in the above formula.
For n=2, we have
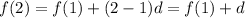
if we replace
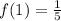 and
and
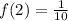 and solve for
and solve for
 we obtain
we obtain

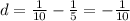
Therefore the explicit form is
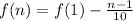 for all
for all
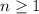 .
.