Answer:
The mean of the total payments she will receive is $79,500.
The standard deviation of the total payments she will receive is $14,000.
Explanation:
Given : An author receives a contract from a publisher, according to which she is to be paid a fixed sum of $20,000 plus $3.50 for each copy of her book sold. The author judges that her uncertainty about total sales of the book can be represented by a random variable with a mean of 17,000 and a standard deviation of 4,000 books.
To find : The mean and standard deviation of the total payments she will receive ?
Solution :
Let 'x' represent total sales of the book.
Let 'y' represent the payment to the author.
According to question,
The mean of the total payments she will receive is given by,
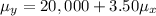
Where,

Substitute in the equation,


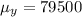
The mean of the total payments she will receive is $79,500.
The standard deviation of the total payments she will receive is given by,
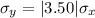
Where,
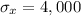
Substitute in the equation,
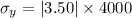
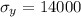
The standard deviation of the total payments she will receive is $14,000.