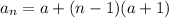Answer:
The explicit form f(n) is
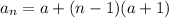
Explanation:
A sequence is arithmetic if the difference between each consecutive terms is a constant.
The explicit formula of an arithmetic sequence is:
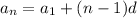
Where d is the common difference, a1 is the first term of the sequence and an is the nth term.
In order to obtain the common difference, you have to subtract two consecutive terms:
For the first and second terms:
2a+1 - a = a+1
For the second and third terms:
3a+2 - (2a+1)=
Applying the distributive property:
3a+2-2a-1= a+1
Notice that the difference of any two consecutive terms is the same. Therefore:
d=a+1
Also, a1=a (The first term)
Replacing in the explicit formula: