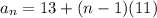Question

Consider the arithmetic sequence 13, 24, 35, ....

a. Find an explicit form for the sequence in terms of n.

Answer 1

The explicit form for the sequence is:
`a_(n)=13+(n-1)(11)`

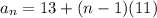
Explanation:

In order to find an explicit form for the given sequence, you have to use the definition of arithmetic sequence and the explicit formula.

An arithmetic sequence is defined as a sequence where the difference of two consecutive terms is a constant.

The explicit formula is:

`a_(n)=a_(1) + (n-1)d`

Where a1 is the first term, d is the common difference and an is the nth term of the sequence.

You have to subtract two consecutive terms to obtain d:

24-13= 11

35-24=11

Therefore d=11

In this case a1=13

Replacing in the formula:

`a_(n)=13+(n-1)(11)`