Question

A water skier lets go of the tow rope upon leaving the end of a jump ramp at a speed of 14.0 m/s. As the drawing indicates, the skier has a speed of 13.0 m/s at the highest point of the jump. Ignoring air resistance, determine the skier’s height above the top of the ramp at the highest point.

Answer 1

1.38 metres

Step-by-step explanation:

Using the law of conservation of energy, the mechanical energy when leaving the ramp is same as mechanical energy when the skier is at the highest point

When leaving the ramp, sum of kinetic energy and potential energy will be

Ei=KEi+PEi where Ei is initial mechanical energy, KEi is initial kinetic energy and Pei is initial potential energy

KEi=
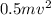`0.5mv^(2)` where v is the initial speed and m is mass

PEi=mgh but since h=0, PEi=0 where m is mass, g is gravitational constant and h is height

Therefore, Ei=KEi+PEi=
`0.5mv^(2)+0=0.5m*14^(2)+0=98m`

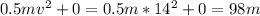
The mechanical energy of the skier at the highest point is given by

Ef=KEf+PEf where Ef is final energy, KEf is final kinetic energy and PEf is final potential energy

Ef=
`0.5mv^(2)+mgh=m(0.5v^(2)+gh)=m(0.5*13^(2)+9.81h)=m(84.5+9.81h)`

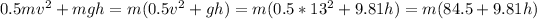
Equating Ei=Ef then

98m= m(84.5+9.81h)

98-84.5=9.81h

h=13.5/9.81= 1.376147m

h=1.38 metres