Answer: The sequence is an arithmetic sequence
The recursive formula is given as
 =
=
 + 7 , where
+ 7 , where
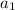 = 14
= 14
Explanation:
 For a sequence to be geometric then there must exist a common ratio. Let r represent the common ratio. The formula for calculating common ratio implies:
For a sequence to be geometric then there must exist a common ratio. Let r represent the common ratio. The formula for calculating common ratio implies:
 r =
r =
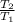 =
=
 … , that is r is calculated by dividing the second term by the first term or the third term divided by the second term and so on.
… , that is r is calculated by dividing the second term by the first term or the third term divided by the second term and so on.
 To check if the sequence is geometric, let us find the common ratio.
To check if the sequence is geometric, let us find the common ratio.

 = 14
= 14

 = 21
= 21

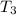 = 28
= 28

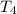 = 35
= 35
 So,
So,
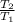 =
=
 =
=


 =
=
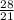 =
=


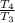 =
=
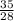 =
=
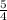
 Considering the result, it is clear that it is not a geometric sequence since the ratios are not the same
Considering the result, it is clear that it is not a geometric sequence since the ratios are not the same
 Arithmetic Sequence , for a sequence to be arithmetic then there must be an existence of a common difference.That is
Arithmetic Sequence , for a sequence to be arithmetic then there must be an existence of a common difference.That is

 –
–
 =
=
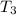 –
–
 =
=
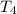 –
–
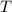
 Let us check if the sequence given follow this rule
Let us check if the sequence given follow this rule

 –
–
 = 21 -14 = 7
= 21 -14 = 7

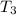 –
–
 = 28 – 21 = 7
= 28 – 21 = 7

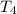 –
–
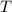 = 35 – 28 = 7
= 35 – 28 = 7
 Therefore the sequence is an arithmetic sequence.
Therefore the sequence is an arithmetic sequence.
 To find the recursive formula for the sequence
To find the recursive formula for the sequence

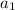 = 14
= 14

 =
=
 +d
+d

 =
=
 +7
+7