Question

A man at point A directs his rowboat due north toward point B, straight across a river of width 100 m. The river current is due east. The man starts across, rowing steadily at 0.75 m/s and reaches the other side of the river at point C, 150 m downstream from his starting point. While the man is crossing the river, what is his velocity relative to the shore?

Answer 1

1.35208 m/s

Step-by-step explanation:

Speed of the boat = 0.75 m/s

Distance between the shores = 100 m

Time = Distance / Speed

`Time=(100)/(0.75)=133.33\ s`

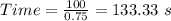
Time taken by the boat to get across is 133.33 seconds

Point C is 150 m from B

Speed = Distance / Time

`Speed=(150)/((100)/(0.75))=1.125\ m/s`

Velocity of the water is 1.125 m/s

From Pythagoras theorem

`c=√(0.75^2+1.125^2)\\\Rightarrow c=1.35208\ m/s`

So, the man's velocity relative to the shore is 1.35208 m/s