Question

In midair an M = 145 kg bomb explodes into two pieces of m1 = 115 kg and another, respectively. Before the explosion, the bomb was moving at 24.0 m/s to the east. After the explosion, the velocity of the m1 = 115 kg piece is 65.0 m/s to the east. Find the velocity (in m/s) (with a proper sign) of the other piece after the explosion

Answer 1

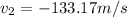`v_2=-133.17m/s`, the minus meaning west.

Step-by-step explanation:

We know that linear momentum must be conserved, so it will be the same before (
`p_i`) and after (
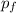`p_f`) the explosion. We will take the east direction as positive.

Before the explosion we have
`p_i=m_iv_i=Mv_i`.

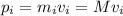After the explosion we have pieces 1 and 2, so
`p_f=m_1v_1+m_2v_2`.

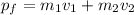These equations must be vectorial but since we look at the instants before and after the explosions and the bomb fragments in only 2 pieces the problem can be simplified in one dimension with direction east-west.

Since we know momentum must be conserved we have:

`Mv_i=m_1v_1+m_2v_2`

Which means (since we want
`v_2` and
`M=m_1+m_2`):

`v_2=(Mv_i-m_1v_1)/(m_2)=(Mv_i-m_1v_1)/(M-m_1)`

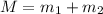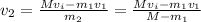
So for our values we have:

`v_2=((145kg)(24m/s)-(115kg)(65m/s))/((145kg-115kg))=-133.17m/s`