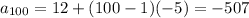Question

Consider a sequence given by the formula an = an−1 − 5, where a1 = 12 and n ≥ 2.

c. Find a6 and a100 of the sequence

Answer 1

a6 = -13

a100 = -507

Explanation:

To find the value for a6 and a100 we first need an explicit formula for the sequence

To find the explicit formula we need to find the first few terms of the sequence (in this case we take the first 5)

To find the first 5 terms we have the initial value
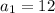`a_(1) = 12` and using the given formula we find the remaining 4 values

the 5 values are as follow

a1 = 12

a2 = 7

a3 = 2

a4 = -3

a5 = -8

From this we know the initial value which is 12 and the constant difference between each value which is -5

Using the general formula for arithmetic sequences i.e.

`a_(n) = a_(1) + (n-1) d`

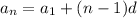
where

`a_(n)` is the nth term of the sequence

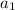`a_(1)` is the initial value which is 12

`n` is the nth count

`d` is the constant difference between each term which is -5

Thus we have the following formula

`a_(n) = 12 + (n-1) (-5)`

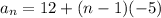
Finding the a6 or 6th value

`a_(6) = 12 + (6-1) (-5) = -13`

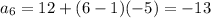
Finding the a100 or 100th value

`a_(100) = 12 + (100-1) (-5) = -507`