Question

Normal Distribution. Cherry trees in a certain orchard have heights that are normally distributed with mu = 112 inches and sigma = 14 inches. What is the probability that a randomly chosen tree is greater than 140 inches? For this problem we want just the answer. Please give up to 4 significant decimal places, and use the proper rules of rounding.

Answer 1

The probability that a randomly chosen tree is greater than 140 inches is 0.0228.

Explanation:

Given : Cherry trees in a certain orchard have heights that are normally distributed with
`\mu = 112` inches and
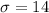`\sigma = 14` inches.

To find : What is the probability that a randomly chosen tree is greater than 140 inches?

Solution :

Mean -
`\mu = 112` inches

Standard deviation -
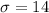`\sigma = 14` inches

The z-score formula is given by,
`Z=(x-\mu)/(\sigma)`

Now,

`P(X>140)=P((x-\mu)/(\sigma)>(140-\mu)/(\sigma))`

`P(X>140)=P(Z>(140-112)/(14))`

`P(X>140)=P(Z>(28)/(14))`

`P(X>140)=P(Z>2)`

`P(X>140)=1-P(Z<2)`

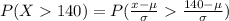
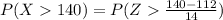
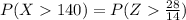
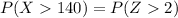
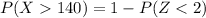
The Z-score value we get is from the Z-table,

`P(X>140)=1-0.9772`

`P(X>140)=0.0228`

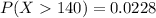
Therefore, the probability that a randomly chosen tree is greater than 140 inches is 0.0228.