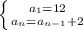Question

Each sequence below gives an explicit formula. Write the first five terms of each sequence. Then, write a recursive

formula for the sequence.
a. an = 2n + 10 for n ≥ 1

Answer 1

The first five values are 12, 14, 16, 18 and 20

The recursive formula is as follow

`\left \{ {{a_(1) =12} \atop {a_(n) =a_(n-1) } + 2} \right.`

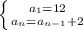
Explanation:

Since we need to find the first 5 values we start with n = 1 to n = 5. Note that we don't start from n = 0 as the question states that n ≥ 1.

For the first 5 values we just replace the value of n with 1, 2, 3, 4 and 5 and calculate the answer

`a_(1)  = 2(1) + 10 = 12\\ a_(2) = 2(2) + 10 = 14\\  a_(3) = 2(3) + 10 = 16\\  a_(4) = 2(4) + 10 = 18\\ a_(5) = 2(5) + 10 = 20`

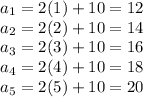
The first five values are 12, 14, 16, 18 and 20

A recursive formula is one that

a) Mentions the initial term

b) provides a formula connecting the previous term to the existing term.

Since we know the first term is 12, i.e
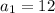`a_(1) = 12` and we know that the difference between consecutive terms is 2 we can conclude that the recursive formula is made up of the following two formulas

`a_(1) = 12`

`a_(n) = a_(n-1)  + 2`

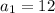
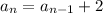
The over all formula is as follow

`\left \{ {{a_(1) =12} \atop {a_(n) =a_(n-1) } + 2} \right.`