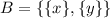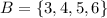Question

If A={1,2,3,4,5},AnB={3,4,5}and sub={1,2,3,4,5,6},find the set B​

Answer 1

`B = \{3,4,5,6\}`

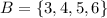
Explanation:

Given

`A = \{1,2,3,4,5\}`

`A\ n\ B = \{3,4,5\}`

`A\ u\ B = \{1,2,3,4,5,6\}`

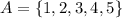
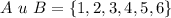
Required

Find set B

`A\ n\ B = \{3,4,5\}` means that the common elements in A and B are 3, 4 and 5.

This implies that:

A subset of B are:

`x = \{3,4,5\}`

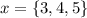
And it also means that
`\{1,2\}` are not elements of B.

The remaining elements (y) of B are then calculated as follows:

`y = (A\ u\ B) - (\{1,2\}\ u\ x)`

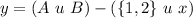
This gives:

`y = \{1,2,3,4,5,6\} - (\{1,2\} u \{3,4,5\})`

`y = \{1,2,3,4,5,6\} - \{1,2,3,4,5\}`

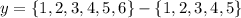
Remove common elements

`y = \{6\}`

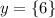
Hence, the set B is:

`B = \{\{x\},\{y\}\}`

`B = \{3,4,5,6\}`