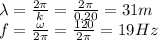Question

wavelength (in meters) and frequency (in hertz) of a wave whose displacement is and t is in seconds? 6) What are the given by the equation y 0.5 sin(0.20x+1201), where x and y are in mete A) 10 m, 0.50 Hz B) 5.0 m, 10 Hz C) 19 m, 120 Hz D) 31 m, 19 Hz E) 0.20 m, 120 2m Hz arn

Answer 1

D) 31 m, 19 Hz

Step-by-step explanation:

The equation of the wave in the problem is

`y = 0.5 sin (0.20 x+120t)`

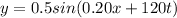
In general, the equation of a travelling wave is written as

`y=Asin(kx+\omega t)`

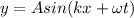
where

A is the amplitude

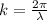`k=(2\pi)/(\lambda)` is the wave number, with
`\lambda` being the wavelength of the wave

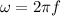`\omega=2\pi f` is the angular frequency and f is the frequency

By comparing the two equations, we see that for this wave:

`k = 0.20 m^(-1)\\\omega = 120 rad/s`

So now we can use the two equations for k and
`\omega` to find the wavelength and the frequency of the wave:

`\lambda=(2\pi)/(k)=(2\pi)/(0.20)=31 m\\f = (\omega)/(2\pi)=(120)/(2\pi)=19 Hz`