Question

The safety inspector in a large city wants to estimate the proportion of buildings in the city that are in violation of fire codes. A random sample of 40 buildings is chosen for inspection, and 4 of them are found to have fire code violations. Estimate the proportion of buildings in the city that have fire code violations, and find the uncertainty in the estimate.

Answer 1

Proportion of buildings in the city that have fire code violations: 10%

Uncertainty 0.3 = 30%

Explanation:

This situation complies with a binomial model where p is the probability of finding a building having fire code violations and q=1-p

Since in random sample of 40 buildings chosen for inspection 4 of them are found to have fire code violations, the proportion is 4/40 = 0.1 or 10% and p=0.1 as well.

In a binomial model the standard deviation s is:

`\large s=√(npq)`

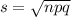
where n is the sample size. So

`\large s=√(40*0.1*0.9)=1.8974`

and the uncertainty is the standard error SE

`\large SE=(s)/(√(n))=(1.8974)/(√(40))=0.3=30\%`