Question

Consider a sequence that follows a times 5 pattern: 1, 5, 25, 125, ….

b. Using the formula, find the 10th term of the sequence.

Answer 1

Answer: 1953125

Explanation:

The given sequence = 1, 5, 25, 125, ….

We can rewrite the terms of the above sequence as (power of 5):

`5^0,\ 5^1,\ 5^2,\ 5^3\ ,....`

Formula for each term :
`f(n)=5^(n-1)`

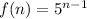
To find the 10th term , we substitute n=10 , we get

`f(10)=5^(10-1)=5^9\\\\=5*5*5*5*5*5*5*5*5\\\\=1953125`

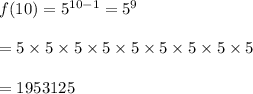
Hence, the 10th term of the sequence.= 1953125