Answer:
The circumference of the circle is 29.36 cm
Explanation:
Let
x -----> the length of first piece (shape of square)
y ------> the length of the other piece (shape of a circle)
we know that
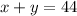
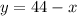 -----> equation A
-----> equation A
step 1
Find out the area of square
The perimeter of square is equal to the length of the first piece
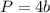
where
b is the length side of square
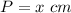
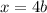
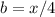
Find the total area A
The area of square is
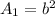
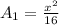
step 2
Find out the area of the circle
The circumference of the circle is equal to the length of the other piece
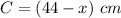
The circumference is equal to
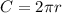
so
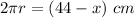
Find the radius of the circle

Find the area of the circle
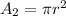
substitute the value of r
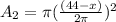
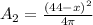
step 3
Find out the total area
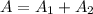
substitute
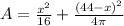
This is a vertical parabola open upward
The vertex is a minimum
using a graphing tool
The vertex is the point (14.64, 67.77)
see the attached figure
For x=14.64 cm -----> the area is a minimum
The lengths of the wire are
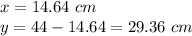
therefore
The circumference of the circle is 29.36 cm