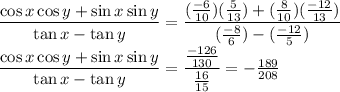Answer:
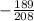
Explanation:
Given
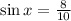
x lies in the second quadrant where sin and cosec is positive and rest trigonometric functions are negative
so,
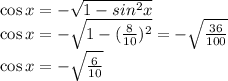
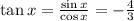
similarly,
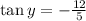
Also, y lies in 4 th Quadrant where cos and sec is positive and rest trigonometric functions are negative
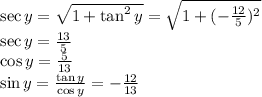
Now putting the values
=