Question

The grower has 250 acres of land available to raise 2 crops, apples and peaches. it takes 1 day to fertilize an acre of apples and two days to fertilize 1 acre of peaches. there are 240 days a year available for fertilizing. find the number acres of each fruit that should be planted to maximize profit. assuming that the profit is $120 per acre of apples and $215 per acre of peaches. find the constants.

Answer 1

The maximum profit will be $28,800 when 240 acres go for apples and 0 acres go for peaches

Explanation:

Let x be the number of acres with apples and y be the numbere of acres with peaches. Note that
`x\ge 0, \ y\ge 0.`

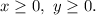
The grower has 250 acres of land available, then

`x+y\le 250`

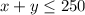
It takes 1 day to fertilize an acre of apples, so it takes x days to fertilize x acres of apples.

It takes 2 days to fertilize 1 acre of peaches, so it takes 2y days to fertilize y acres of peaches.

There are 240 days a year available for fertilizing, so

`x+2y\le 240`

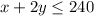
The profit is $120 per acre of apples and $215 per acre of peaches, then the total profit is

`P=120x+215y`

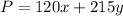
We get the function
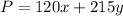`P=120x+215y` which must maximized using restrictions

`\left\{\begin{array}{l}x\ge 0\\y\ge 0\\x+y\le 250\\ x+2y\le 240\end{array}\right.`

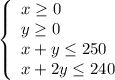
Show the solution set of this system of inequalities graphically.

The maximum profit can be at the vertices of this region:

`P(0,120)=120\cdot 0+215\cdot 120=\$25,800\\ \\P(240,0)=120\cdot 240+215\cdot 0=\$28,800`

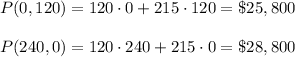
The maximum profit will be $28,800 when 240 acres go for apples and 0 acres go for peaches