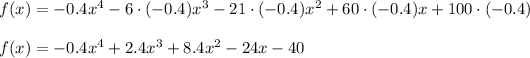Answer:

Explanation:
If -2 and 5 are double roots of the polynomial function, then the function expression is
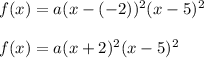
Rewrite this function in standard form:
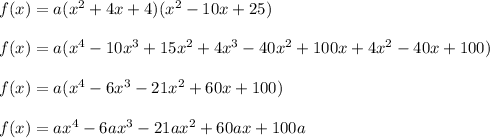
The constant term of the polynomial in standard form is -40, so

Therefore, the function expression is