Question

Prism M and pyramid N have the same base area and the same height. Cylinder P and prime Q have the same height and the same bass perimeter. Cone Z has the same base area as the Cylinder Y, but it’s height is three times the height of the cylinder Y.

Answer 1

Cone Z and Cylinder Y

Explanation:

Complete Question:

Prism M and pyramid N have the same base area and the same height. Cylinder P and prism Q have the same height and the same base perimeter. cone Z has the same base area as cylinder Y, but its height is three times the height of cylinder Y. Which two figures have the same volume?

Solution:

Volume of Cone is given by
`V_(cone)=(1)/(3)\pi r^2 h`

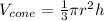
Volume of Cylinder is given by
`V_(cylinder)=\pi r^2 h`

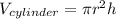
It is given Cone Z has height that is 3 times that of Cylinder Y. Let Cylinder Y have height h ( from formula ), so Cone Z will have height "3h". So, Volume of Cone Z would be now:

`V_(cone)=(1)/(3)\pi r^2 h\\V_(cone)=(1)/(3)\pi r^2 (3h)\\V_(cone)= \pi r^2 h`

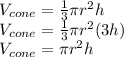
Which is same as Volume of Cylinder Y!!

Thus, we can say Cone Z and Cylinder Y have same volume.