Question

For a certain interval of time, an object is acted upon by a constant non-zero force. Which of the following statements is true for this interval of time?

Answer 1

Missing options:

a. The object is accelerating.

b. The object's velocity can only increase.

c. The object is at rest.

d. The object is moving with constant velocity.

e. The object's velocity changes.

Answer:

a. The object is accelerating.

e. The object's velocity changes.

Step-by-step explanation:

Let's answer by using Newton's second law:

`F = ma`

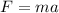
where

F is the net force on the object

m is the mass of the object

a is the acceleration

From the equation, we see that if the force on an object is non-zero, then the object is for sure accelerating, since
`a` is different from zero.

So, option A is correct.

Now, we also recall the definition of acceleration, which is the rate of change of velocity:

`a=(\Delta v)/(\Delta t)`

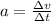
where
`\Delta v` is the change in velocity in the time interval
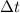`\Delta t`. This can be rewritten as

`\Delta v = a \Delta t`

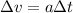
Here, since the acceleration is non-zero, it follows that also
`\Delta v\\eq 0`: which means that the velocity of the object is changing.

So, option E is also correct.

The other options are wrong because:

b. The object's velocity can only increase. --> false, in fact acceleration can also be negative, and in that case the velocity would be decreasing

c. The object is at rest. --> false, since the velocity of the object is changing

d. The object is moving with constant velocity. --> false, since the velocity of the object is changing