Answer:
x=
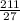
Y=
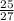
Explanation:
For solving the two variable linear equation by Cramer's rule we have to find the determinant .
here, determinant D =
![\left[\begin{array}{ccc}5&1\\2&-5\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rmrpjdv2os2c2ecc09leu7dsfnidcbyqhu.png)
D=(5 × (-5)) - (2 × 1)
D = (-25)-(2)
D= -27
Now again we have to find the determinant with sub X and determinant with sub Y
Determinant with sub X ( Dx)
Dx=
![\left[\begin{array}{ccc}40&1\\11&-5\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/854q00sd4vfbut1ax32aadax8i0u7caufb.png)
Dx= ((40×(-5)) - (11×1)
Dx= -200-11
Dx= -211
now Determinant with sub Y Dy
Dy=
![\left[\begin{array}{ccc}5&40\\2&11\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3xgvvpo6dpuruascclxw8jh9ax6gir2dwy.png)
Dy=(5×11)-(2×40)
Dy=(55-80)
Dy=-25
now to find the values of variables X and Y, we have to write
X=
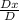
or X=
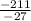
and
Y=
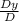
i.e Y=
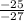
form here we got the value of variable X and Y (Answer)