Question

Find the liner equation from this information Passing through the
points (4,-9) & (2,-4)​

Answer 1

The equation is 2y + 5x = 2

Explanation:

The two points given are (x1 , y1) = (4,-9) and (x2 , y2) = (2,-4)

Step 1: find out the slope of the equation

Slope m of any equation =
`\frac{y_(2) - y{1}}{x_(2) - x_(1)}}  = (-4-(-9))/(2 -4)  = (-4 + 9)/(-2)  = -(5)/(2)`

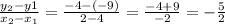
Hence, m = (-5/2)

Step 2: Substitue m in the equation y = mx + b

⇒
`y = (-5)/(2) x+ b \\ or, 2y + 5x = b`

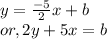
Step 3: put any of the two points in above equation and find y-intercept b

⇒Using (2,-4), we get 2y + 5x = 2(-4) + 5 (2) = -8 + 10 = 2

⇒ b = 2

Step 4: Substitute the value of b in the above equation

we get, 2y + 5x = b = 2

Hence, the equation is 2y + 5x = 2