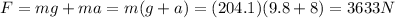Question

A box weighs 2000N and is accelerated uniformly over a horizontal surface at a rate of 8 m/s^2. The opposing force of friction between the box and the surface is 27.4.

How much force would be required to lift the box upward with an acceleration of 8 m/s^2?

Answer 1

3633 N

Step-by-step explanation:

When the box is lift upward, there are only two forces acting on it:

- The force of push, F, upward

- The force of gravity, downward, which is the weight of the object:

W = 2000 N

So, the equation of motion for the box is

`F-W = ma`

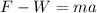
where

m is the mass of the object

a is its acceleration

The mass can be found from the weight of the box:

`m=(W)/(g)=(2000)/(9.8)=204.1 kg`

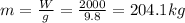
Where g = 9.8 m/s^2 is the acceleration of gravity, and the acceleration is

`a=8 m/s^2`

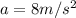
So, we can solve for F, the force required:

`F=mg+ma=m(g+a)=(204.1)(9.8+8)=3633 N`