Question

A fuzzy bunny sees a butterfly and chases it right off of a 20 m high cliff at 7m/s

A)how long did it take the bunny to be dashed among the rocks?
B)how far from the base did the bunny hit the ground?
C)what was the velocity and angle of impact of the fuzzy mammal when it hit the ground?

Answer 1

A) 2.02 s

To find the time it takes for the bunny to reach the rocks below the cliff, we just need to analyze its vertical motion. This motion is a free fall motion, which is a uniformly accelerated motion. So we can use the suvat equation:

`s=u_y t+(1)/(2)at^2`

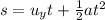
where

s is the vertical displacement

u is the initial vertical velocity

a is the acceleration

t is the time

For the bunny here, choosing downward as positive direction,

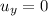`u_y = 0` (initial vertical velocity is zero)

s = 20 m

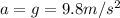`a=g=9.8 m/s^2` (acceleration of gravity)

And solving for t, we find the time of flight:

`t=\sqrt{(2s)/(g)}=\sqrt{(2(20))/(9.8)}=2.02 s`

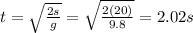
B) 14.1 m

For this part, we need to consider the horizontal motion of the bunny.

The horizontal motion of the bunny is a uniform motion with constant velocity, which is the initial velocity of the bunny:

`v_x = 7 m/s`

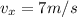
Therefore the distance covered after time t is given by

`d=v_x t`

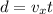
And substituting the time at which the bunny hits the ground,

t = 2.02 s

We find how far the bunny went from the cliff:

`d=(7)(2.02)=14.1 m`

C) 21.0 m/s at
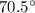`70.5^(\circ)` below the horizontal

The horizontal component of the velocity is constant during the entire motion, so it will still be the same when the bunny hits the ground:

`v_x = 7 m/s`

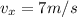
Instead, the vertical velocity is given by

`v_y = u_y +at`

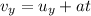
And substituting t = 2.02 s, we find the vertical velocity at the moment of impact:

`v_y = 0+(9.8)(2.02)=19.8 m/s`

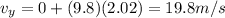
So, the magnitude of the final velocity is

`v=√(v_x^2+v_y^2)=√(7^2+(19.8)^2)=21.0 m/s`

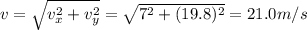
And the angle is given by

`\theta=tan^(-1)((v_y)/(v_x))=tan^(-1)((19.8)/(7))=70.5^(\circ)`

below the horizontal