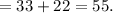Question

At a baseball game, there were three times as many males as females, 5/6 of the males were boys and the rest were men, 2/3 of the females were girls and the rest were women. Given that there were 121 more boys than the girls, how many adults were there at the baseball game?

Answer 1

55

Explanation:

Let x be the number of females at a baseball game. There were three times as many males as females, then the number of males is 3x.

5/6 of the males were boys and the rest were men, then

• 
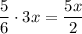  `(5)/(6)\cdot 3x=(5x)/(2)` is the number of boys;
• 
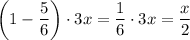  `\left(1-(5)/(6)\right)\cdot 3x=(1)/(6)\cdot 3x=(x)/(2)` is the number of men.

2/3 of the females were girls and the rest were women, then

• 
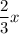  `(2)/(3)x` is the number of girls;
• 
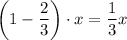  `\left(1-(2)/(3)\right)\cdot x=(1)/(3)x` is the number of women.

There were 121 more boys than the girls, thus

`(5x)/(2)-(2x)/(3)=121\\ \\(5x\cdot 3-2x\cdot 2)/(6)=121\\ \\15x-4x=121\cdot 6\\ \\11x=726\\ \\x=66`

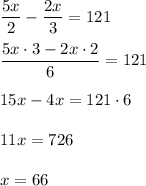
There were 66 females and 198 males.

The number of men
`=(66)/(2)=33;`

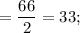
The number of women
`=(66)/(3)=22;`

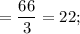
The total number of adults
`=33+22=55.`