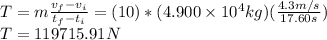Question

An engine pulls a train of 20 freight cars, each having a mass of 4.900 × 104 kg, with a constant force. The cars move from rest to a speed of 4.300 m/s in 17.60 s on a straight track. Neglecting friction, what is the force with which the tenth car pulls the eleventh one (at the middle of the train)?

Answer 1

The force with which the tenth car pulls the eleventh one is called tension and is equal to:

T=119715.91 N

Step-by-step explanation:

The force (F) with which the tenth car pulls the eleventh one is called tension and its direction is the X-direction or horizontal. According to Newton's Second Law of motion:

`\sum F=ma`

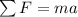
That is, the force of the car is equal to the acceleration (a) times its mass (m). The acceleration is the change in the velocity divided by the time (i is for initial and f is for final).

`a=(v_f-v_i)/(t_f-t_f)`

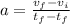
Using Newton's second law:

To find the forces, you have to solve the equilibrium in X-direction:

`\sum F_x=T=ma_x`

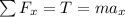
Now you can substitute the accelertion in terms of velocity and time:

`\sumF_x=T=ma_x=m(v_f-v_i)/(t_f-t_i)`

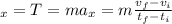
Solve the equation using the data from the problem, remember that the mass of the object is 10 times the mass of one car because the 10th car has to pull all the other cars:

`T=m(v_f-v_i)/(t_f-t_i)=(10)*(4.900 * 10^4 kg)((4.3 m/s)/(17.60s))\\T=119715.91 N`