Question

NASA’s mission Juno is currently orbiting Jupiter. The most recent full orbit Juno made (as measured between the times of closest approaches to Jupiter) started on July 21, 2019 and ended on September 12, 2019. You can assume that both passages happened at the same time, e.g. at 6 am. What is the semi-major axis of the orbit of Juno around Jupiter, expressed in kilometers?

Answer 1

`a=4066435km`

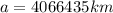
Step-by-step explanation:

Kepler's 3rd Law tells us that:

`a^3=((GM)/(4\pi^2))T^2`

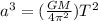
where a is the semi-major axis, M the mass of the much more massive central object (in this case Jupiter, so
`M=1.898*10^(27)Kg`), T the orbital period and
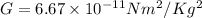`G=6.67*10^(-11)Nm^2/Kg^2` the gravitational constant.

If we count the days between July 21, 2019 and September 12, 2019 we get 53 days , from there we can calculate the seconds easily by doing 53(24)(60)(60), obtaining 4579200 seconds. We put this then in our equation:

`a=\sqrt[3]{((GM)/(4\pi^2))T^2}=\sqrt[3]{(((6.67*10^(-11)Nm^2/Kg^2)(1.898*10^(27)Kg))/(4\pi^2))(4579200s)^2}=4066435070m=4066435km`