Question

A spherical water drop 1.5 μm in diameter is suspended in calm air due to a downward-directed atmospheric electric field of magnitude E = 640 N/C. (a) What is the magnitude of the gravitational force on the drop? (b) How many excess electrons does it have?

Answer 1

(a)
`F_(G) = 5.51* 10^(- 15) N`

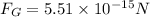
(b) 54 electrons in excess

Solution:

As per the question:

Diameter of the spherical drop, d =
`1.5\mu m = 1.5* 10^(- 6)m`

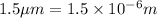
Magnitude of the Electric field, E = 640 N/C

Now,

(a) The magnitude of the gravitational force on the spherical drop is given by using Newton's second law:

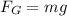`F_(G) = mg` (1)

where

m = mass of the sphere

g = acceleration due to gravity

Also,

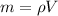`m = \rho V` (2)

where

`\rho` = density of the spherical water drop =
`1000 kgm^(- 3)`

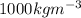
V = volume of the sphere =
`(4)/(3)\pi ((d)/(2))^(3)`

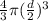
Now, eqn (2) becomes:

`m = \rho (4)/(3)\pi ((d)/(2))^(3)`

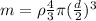
Thus eqn (1) will be:

`F_(G) = \rho (4)/(3)\pi ((d)/(2))^(3)g`

`F_(G) = 1000* (4)/(3)\pi ((1.5* 10^(- 6))/(2))^(3)* 9.8`

`F_(G) = 5.51* 10^(- 15) N`

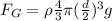
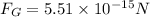
(b) No. of excess electron:

Now, the spherical drop is suspended in the air, both the electrostatic and gravitational forces on the drop must be equal:

Electrostatic force,
`F_(E) = QE = neE`

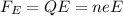
where

Q = charge = ne

n = no. of electrons

e = electronic charge

Now,

`F_(G) = F_(E)`

`5.51* 10^(- 15) = neE`

`5.51* 10^(- 15) = n* 1.6* 10^(- 19)* 640`

`n = {5.51* 10^(- 15)}{1.6* 10^(- 19)* 640}`

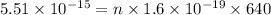
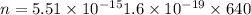
n = 53.8 ≈ 54 electrons