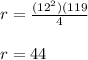Answer:
Explanation:
The combine variation equation will have the folllowing form:
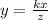
Where "k" is the constantn of variation.
You know that "r" varies directly as the square of "m", and inversely as "s". Then the equation is:
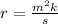
Knowing that
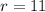 when
when
 and
and
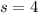 , you can substitute values into the equation and solve for "k" in order to find its value:
, you can substitute values into the equation and solve for "k" in order to find its value:
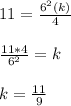
Now, to find the value of "r" when
 and
and
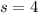 , you need tot substitute these values and the the constant of variation into
, you need tot substitute these values and the the constant of variation into
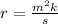 and then evaluate:
and then evaluate: