Question

Frank is lending $1,000 to Sarah for two years. Frank and Sarah agree that Frank should earn a 2 percent real return per year. Instructions: Enter your responses as as whole numbers. a.The CPI (times 100) is 100 at the time that Frank makes the loan. It is expected to be 110 in one year and 121 in two years. What nominal rate of interest should Frank charge Sarah? The nominal rate of interest charged should be %. b. Suppose Frank and Sarah are unsure what the CPI will be in two years. How should Frank index Sarah’s annual repayments to ensure that he gets an annual 2 percent real rate of return. Frank should charge Sarah % the inflation rate.

Answer 1

Frank should charge Sarah a nominal interest rate of 12%. If Frank and Sarah are unsure about the future CPI, Frank should charge Sarah an interest rate equal to 10% of the inflation rate.

Step-by-step explanation:

Given that the Consumer Price Index (CPI) is expected to be 100 at the time of the loan and 110 in one year, we can calculate the expected inflation rate over one year as follows:

(110 - 100) / 100 = 0.10, or 10%

Since Frank wants to earn a 2% real return per year, we can calculate the nominal interest rate as the sum of the real return and the inflation rate:

Nominal interest rate = Real return + Inflation rate

Nominal interest rate = 2% + 10% = 12%

Therefore, Frank should charge Sarah a nominal interest rate of 12%.

If Frank and Sarah are unsure about the future CPI, Frank can index Sarah's annual repayments to ensure he gets a 2% real rate of return. This means that Sarah's repayments will increase by the inflation rate each year. Thus, Frank should charge Sarah an interest rate equal to the expected inflation rate, which is 10% in this case.

Therefore, Frank should charge Sarah an interest rate equal to 10% of the inflation rate.

Answer 2

a. 23%.

b. Frank should charge Sarah 2% more than the inflation rate.

Step-by-step explanation:

a. Find the nominal rate of interest.

To find this value we must follow this equation:

`NI=RI+IR`

Where NI = Nominal Interest, RI= Real Interest, and IR= Inflation Rate.

a.1. Find the real interest rate.

The problem statement gives us this value: 2% real return per year, as agreed by Sarah and Frank.

a.2. Find the inflation rate.

Here we follow this equation:

`IR=((CPI_(F) -CPI_(B) )/(CPI_(B) ) )*100`

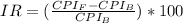
Where:

CPI(F) is the CPI of the final year, in this case, it would be 121 (the expected CPI for two years, which is the established loan time).

CPI (B) is the CPI of the base year, that is, the CPI in force at the time that Frank makes the loan, 100 in this case.

We replace these values:

`IR=((121-100)/(100) )*100`

`IR=((21)/(100) )*100`

`IR=0.21*100`

`IR=21%`

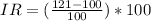
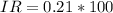
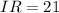
The inflation rate equals 21%.

a.3. Replace in the equation of the nominal rate of interest.

`NI=RI+IR`

`NI=0.02+0.21`

`NI=0.23`

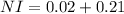
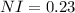
So, the nominal rate of interest Frank should charge Sarah equals 23%.

b. Find out how much Frank should charge Sarah (regarding inflation and considering that it is unknown).

The inflation rate reduces the return expected by Frank. Therefore, the nominal interest rate charged must be higher than the inflation rate, in order to ensure a positive real returns. In this case, since it is not known exactly what that inflation rate is, Frank must charge 2% (expected return) above what the inflation rate can record.

Hence, the short answer is: Frank should charge Sarah 2% more than the inflation rate.