Question

A body of mass 4.5 kg makes an elastic collision with another body at rest and continues to move in the original direction but with 1/5 of its original speed. (a) What is the mass of the other body? (b) What is the speed of the two-body center of mass if the initial speed of the 4.5 kg body was 8.9 m/s?

Answer 1

Answer with Explanation:

We are given that

Mass of one body=4.5 kg

Initial velocity of one body=8.9 m/s

Initial velocity of another body=0

Final velocity of one body=
`(1)/(5)* 8.9=1.78 m/s`

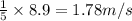
a.We have to find the mass of the other body.

Energy and momentum are conserved in this system

`p_i=P_f`

`m_1v_(1i)+0=m_1v_(1f)+m_2v_(2f)`

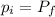
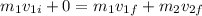
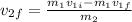`v_(2f)=(m_1v_(1i)-m_1v_(1f))/(m_2)` (equation I)

From conservation of kinetic energy

`(1)/(2)m_1v^2_(1i)=(1)/(2)m_1v_(1f)^2+(1)/(2)m_2v^2_(2f)`

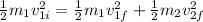
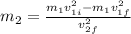`m_2=(m_1v^2_(1i)-m_1v^2_(1f))/(v^2_(2f))` (equation II)

Substitute equation I in equation II

`m_2=(m_1v^2_(1f)-m_1v^2_(1f))/(((m_1v_(1i)-m_1v_(1f))/(m_2))^2)`

`m_2=((m_1v_(1i)-m_1v_(1f))^2)/(m_1v^2_(1i)-m_1v^2_(1f))`

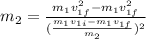
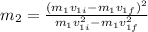
Substitute the given values then we get

`m_2=((4.5* 8.9-4.5* 1.78)^2)/(4.5* (8.9)^2-4.5* (1.78)^2)`

`m_2=3 kg`

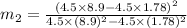
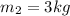
Hence, the mass of other body=3 kg

b.We have to find the speed of two body center of mass .

The center of mass speed is given by

`v_(com)=(p_i)/(m_1+m_2)`

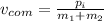
Substitute the values then we get

`v_(com)=(m_1v_1+0)/(m_1+m_2)`

`v_{com=(4.5* 8.9)/(4.5+3)=5.34 m/s`

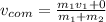
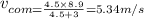
Hence, the speed of the two body center of mass is given by =5.34 m/s