Given:
A piecewise function
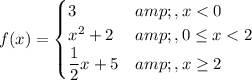
To find:
The range of the function.
Solution:
Range is the set of output values.
For
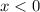 , the function is
, the function is
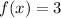 ...(i)
...(i)
For
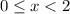 , the function is
, the function is
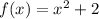 .
.
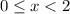
Squaring each side.
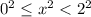
Adding 2 on each side.
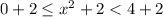
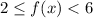 ...(ii)
...(ii)
For
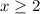 , the function is
, the function is
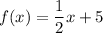 .
.
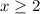
Divide both sides by 2.
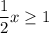
Adding 5 on each side.
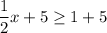
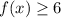 ...(iii)
...(iii)
From (i), (ii) and (iii), it is clear that the values of f(x) lies in the interval [2,∞).
So, the range of the given function is [2,∞).
Therefore, the correct option is b.