Question

Tom scored 77 out of a possible 100 on his midterm math examination. The distribution of the class had a mean of 68 and a standard deviation of 8.8. Peter, who is in a different calculus class, scored 78 out of a possible 100. His class distribution had a mean of 68 and a standard deviation of 16. Relative to the performance of their classes, who did better?

Answer 1

Tom did better relative to the performance of their classes.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

This score how many standard deviations above or below the mean a measure is.

In this problem, whoever has the best Z score between Tom and Peter did better on the test relative to the performance of their classes.

Tom

Scored 77 out of a possible 100 on his midterm math examination. The distribution of the class had a mean of 68 and a standard deviation of 8.8.

So
`X = 77, \mu = 68, 8.8`

`Z = (X - \mu)/(\sigma)`

`Z = (77 - 68)/(8.8)`

`Z = 1.02`

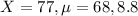
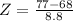
Peter

Scored 78 out of a possible 100. His class distribution had a mean of 68 and a standard deviation of 16.

So
`X = 78, \mu = 68, 16`

`Z = (X - \mu)/(\sigma)`

`Z = (78 - 68)/(16)`

`Z = 0.625`

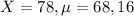
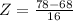
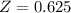
Tom had the higher Z score, so he did better relative to the performance of their classes.