Question

asked May 15, 2020 157k views

1 Answer

Pmoule · Answer 1 · 2020-05-19T17:43:40+0000

Answer:

A Poisson model seems reasonable for this problem, since we have the mean during the time interval.

There is a 1.9% probability that the number of autos entering the tunnel during a two-minute period exceeds three.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

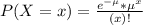
$P(X = x)=(e^(-\mu)*\mu^(x))/((x)!)$

In which

x is the number of sucesses

e = 2.71828 is the Euler number

$\mu$ is the mean in the given time interval.

The mean number of automobiles entering a mountain tunnel per two-minute period is one.

This means that
$\mu = 1$ .

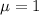For a Poisson model to be reasonable, we only need the mean during the time interval. So yes, a Poisson model seems reasonable for this problem.

Find the probability that the number of autos entering the tunnel during a two-minute period exceeds three.

We want to find
P(X>3)

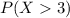
Either this number is less or equal to 3, or it exceeds 3. The sum of the probabilities is decimal 1. So:

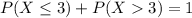
$P(X \leq 3) + P(X > 3) = 1$

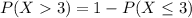
$P(X > 3) = 1 - P(X \leq 3)$

In which

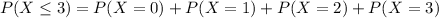
$P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)$

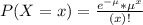
$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

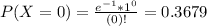
P(X = 0) = (e^(-1)*1^(0))/((0)!) = 0.3679

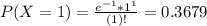
P(X = 1) = (e^(-1)*1^(1))/((1)!) = 0.3679

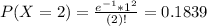
P(X = 2) = (e^(-1)*1^(2))/((2)!) = 0.1839

P(X = 3) = (e^(-1)*1^(3))/((3)!) = 0.0613

So

$P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0.3679 + 0.3679 + 0.1839 + 0.0613 = 0.981$

Finally

$P(X > 3) = 1 - P(X \leq 3) = 1 - 0.981 = 0.019$

There is a 1.9% probability that the number of autos entering the tunnel during a two-minute period exceeds three.

Please log in or register to add a comment.