Question

NASA’s Ames research center in Mountain View, California has a centrifuge built to simulate high-g environments. It spins horizontally in uniform circular motion, with the payload (possibly a human!) in a box at the end of a 29-foot arm. Its maximum rotation rate is 50 revolutions per minute (rpm). (a) What is the centripetal acceleration experienced by an object in the payload box when it is spinning at its maximum rate? (b) How many gs is this acceleration, and could a human survive it (take the maximum survivable g-force to be 8g). (c) What would the rotation rate be to produce this maximum g-force of 8g?

Answer 1

a)
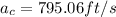`a_(c)=795.06 ft/s`, b) approximately 25g's, c) 28.46 rpm

Step-by-step explanation:

In order to solve this problem, we must first do a drawing of the situation to better visualize it (look at attached picture).

a)

Now, the very first thing we must do is convert the frequency to angular speed, we can do this like this:

`\omega = (50rev)/(s)*(2\pi rad)/(1 rev)*(1min)/(60s)`

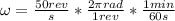
so we get that:

`\omega=5.236 rad/s`

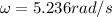
once we have the angular speed, we can use it to find the centripetal acceleration by using the following formula:

`a_(c)=\omega^(2)r`

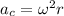
which yields:

`a_(c)=(5.236rad/s)^(2)(29ft)=795.06 ft/s^(2)`

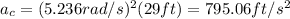
b)

we can use it to figure out how many g's this represents, we know that:

`1g=32.2ft/s^(2)`

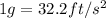
so, we can do the conversion

`795.06ft/s^(2)*(1g)/(32.2ft/s^(2))=24.69g's`

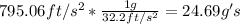
so we have approximately 25 g's on the machine.

c)

In order to produce a maximum acceleration of 8g's we can do the following.

First, turn the 8g's to
`ft/s^(2)`

`8g*(32.2ft/s^(2))/(1g)=257.6ft/s^(2)`

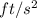
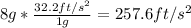
next, we use the same formula, but this time we solve for the angular speed:

`a_(c)=\omega^(2)r`

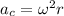
which solves to:

`\omega=\sqrt{(a_(c))/(r)}`

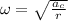
and substitute the provided data:

`\omega=\sqrt{(257.6ft/s^(2))/(29ft)}`

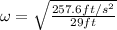
which yields:

`\omega=2.98rad/s`

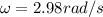
we can use this to find our frequency, like this:

`f=2.98rad/s*(1rev)/(2\pi rad)*(60s)/(1min)=28.46rev/min`

so the frequency the machine should have to reach an acceleration of 8g's is:

f=28.46rpm