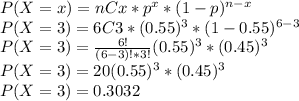Question

Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability of success on a single trial

n=6, x=3,p= 0.55

Answer 1

0.3032

Explanation:

3 parameters [n,x,p] are given. We simply need the formula for binomial distribution and put in the values and solve.

The binomial distribution formula:

`P(X=x)=nCx*p^(x)*(1-p)^(n-x)`

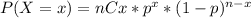
Where nCx is the combination formula.

Now, we put the numbers and solve:

`P(X=x)=nCx*p^(x)*(1-p)^(n-x)\\P(X=3)=6C3*(0.55)^(3)*(1-0.55)^(6-3)\\P(X=3)=(6!)/((6-3)!*3!)(0.55)^3*(0.45)^3\\P(X=3)=20(0.55)^3*(0.45)^3\\P(X=3)=0.3032`